Progetto del profilo di una camma di distribuzione – Progetto del profilo di una camma di distribuzione – La determinazione dell’esatto profilo di una camma di distribuzione è un elemento essenziale ai fini di una corretta progettazione del lato aspirazione di un nuovo motore.
Per prima cosa bisogna calcolare la legge di moto di una valvola di aspirazione di un motore a 4 tempi. Sarà quindi necessario disegnare i grafici di accelerazione, velocità e posizione in forma dimensionale e adimensionale, e valutare i coefficienti di accelerazione e velocità Ca+, Ca– e Cv. Una corretta progettazione del sistema di distribuzione prevede, infatti, il contenimento delle forze d’inerzia, delle dissipazioni di potenza e dell’insorgere di fenomeni vibratori, quindi sarà necessario limitare le accelerazioni del sistema, in particolar modo quelle negative, e garantire un buon grado di continuità tra la fase di lavoro e quella di riposo della valvola.
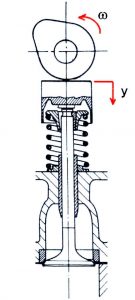
La legge di moto di una valvola è descritta da una funzione del tempo Y=Y(t). Allora la sua velocità e accelerazione sono:
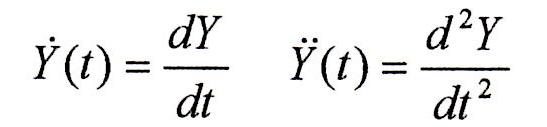
Ipotizzando una velocità di rotazione della camma costante è possibile sostituire al tempo l’angolo di rotazione della camma giungendo alla determinazione della velocità e accelerazione geometriche (Y’ , Y”):
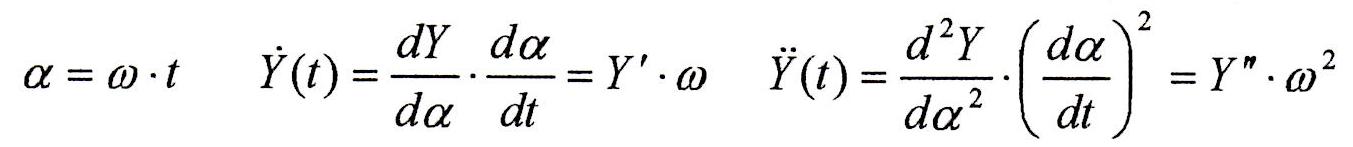
La legge di moto deve consentire alla valvola di passare da alzata nulla (Y=0) a quella massima (Y=h) in un tempo tscorrispondente da un angolo αs.
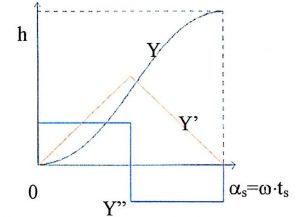
Il grafico dell’accelerazione è quello di maggiore interesse in quanto ad esso sono legate le forze di inerzia, le vibrazioni, etc… Esso ha la proprietà che l’area sottesa della parte con accelerazione positiva è uguale a quella con accelerazione negativa, dovendo il movimento arrestarsi nelle posizioni estreme. Le grandezze significative nel grafico delle accelerazioni sono i valori massimi e minimi:
coefficiente di accelerazione positiva Ca+ = max (y”) coefficiente di accelerazione negativa Ca– = – min (y”)
Se facciamo alcune considerazioni sulle forze in gioco nella fase di apertura e chiusura delle valvole, risulta evidente che minori sono tali coefficienti minore è la forza di inerzia dovuta al movimento del cedente (la valvola). In particolare risulta più conveniente avere un Ca– < Ca+ perché le forze di inerzia dovute ad accelerazioni negative tendono a distaccare il cedente dalla camma e devono quindi essere bilanciate da una molla: per cui se avessimo Ca– elevato dovremmo anche avere molle più grosse e più pesanti. Un altro dato interessante è il massimo valore della velocità: coefficiente di velocità Cv = max (y’)
Anche tale coefficiente deve essere limitato il più possibile poiché da esso dipende la potenza assorbita per spostare il cedente oltre che le dimensioni della camma e del piattello. Abbiamo così determinato le tre grandezze che ci permetteranno di scegliere la migliore legge d’alzata possibile per la valvola:
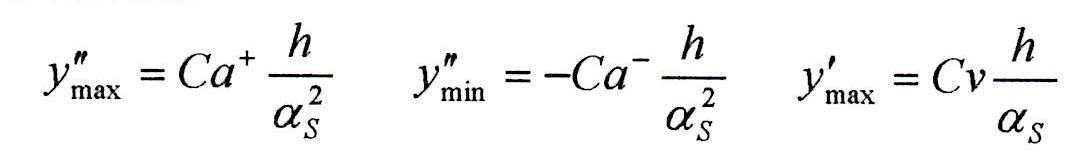
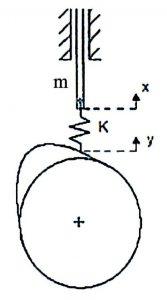
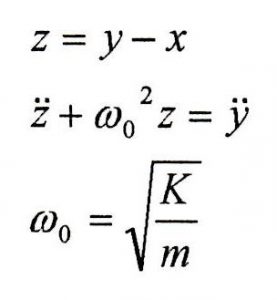
La legge di moto, infine, deve essere tale da limitare al massimo l’insorgenza delle vibrazioni che causano una differenza di tra la posizione voluta e quella effettiva compromettendo il corretto funzionamento della valvola. Considerando infatti la rigidezza dei vari elementi interposti tra camma e valvola si ottengono le seguenti relazioni:
L’errore z tra posizione prevista y e quella effettiva x dipende dal valore dell’accelerazione y che deve perciò essere il più uniforme possibile.
Passiamo ora alle specifiche di progetto utilizzate:
| Alzata massima della valvola h | tra 7 e 11 mm |
| Angolo motore di anticipo apertura αA | tra 5° e 15° |
| Angolo motore di ritardo chiusura αR | tra 35° e 65° |
| Massima velocità di rotazione del motore nMAX | maggiore di 6000 rpm |
e ricordiamo che attualmente leggi di moto effettivamente realizzabili presentano valori dei coefficienti pari a: Ca+< 12; Ca– < 4; Cv < 2.
Per il calcolo della legge di moto imposta al cedente si è utilizzata la seguente relazione di tipo polinomiale a tre coefficienti, in funzione delle variabili adimensionali y e x (ottenute come y = Y/h e x = α/αs, rispettivamente il rapporto tra l’alzata effettiva (Y) e quella massima (h) e il rapporto tra l’angolo effettivo (α) e l’angolo di salita (αs)):
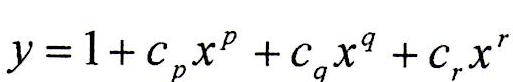
Dove i valori p, q ed r sono scelti tra alcune terne proposte e permettono di ricavare i coefficienti Cp, Cq, Cr. La legge di moto polinomiale ha validità nel campo -1<x<-1 e l’angolo di salita αs si ottiene dalla seguente relazione:
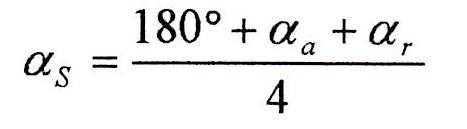
Dove αa e αr sono rispettivamente gli angoli motore di anticipo apertura e ritardo chiusura della fase. I valori di p, qed r scelti sono: p = 2; q = 10; r = 12. Con tali valori abbiamo ottenuto i seguenti coefficienti della legge di moto: Cp = -1,5; Cq = 1,5; Cr = -1 ricavando di conseguenza i grafici adimensionali di posizione, velocità e accelerazione:
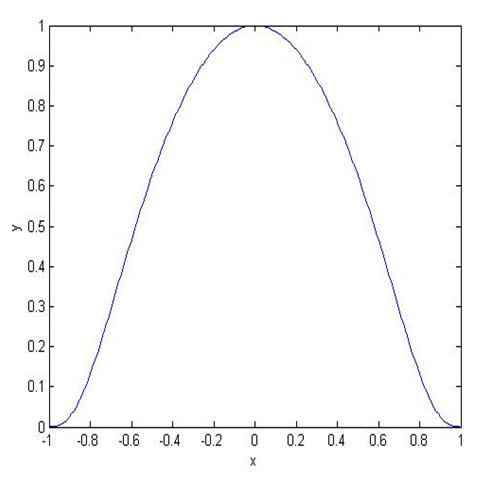
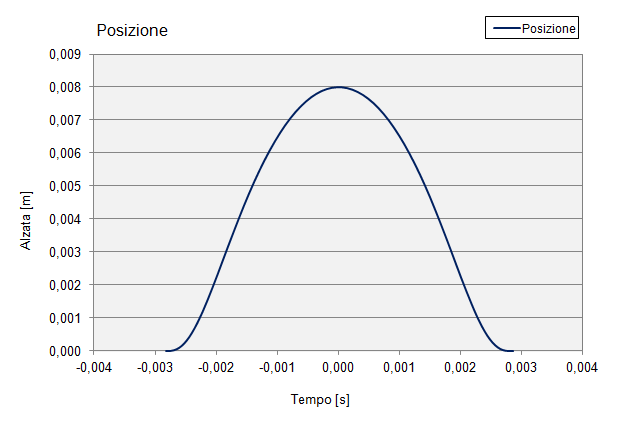
Grafico adimensionale di posizione del cedente: per contenere le accelerazioni la salita e la discesa sono simmetriche e non vi è un tratto di arresto nel punto di massima alzata (x = 0). Un movimento graduale tra la parte dell’alzata (-1<x<+1) e la zona di quiete (y = 0) garantisce una bassa quantità di vibrazioni, che si traduce in minori sollecitazioni del cedente.
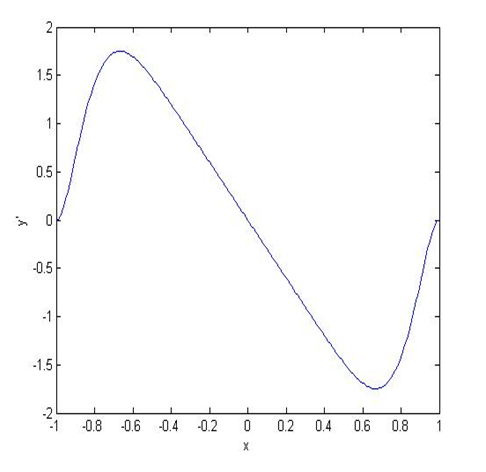
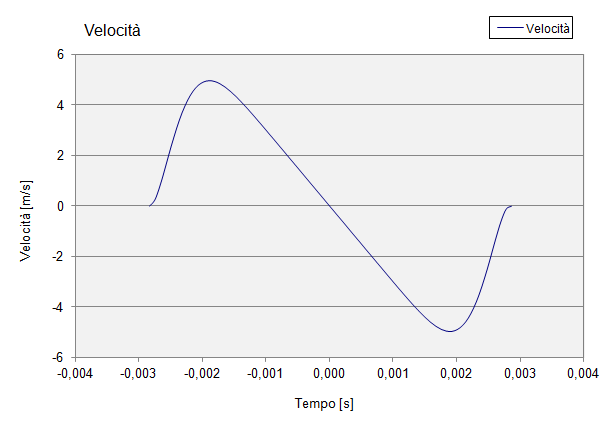
Grafico adimensionale della velocità della valvola: dal punto di massimo assoluto del grafico si ricava il valore del coefficiente di velocità Cv —> Cv = max (y’). Nel nostro caso il coefficiente ha valore Cv = 1,748. Proprio da tale coefficiente dipende la potenza assorbita per spostare il cedente, quindi anche le dimensioni di camma e piattello.
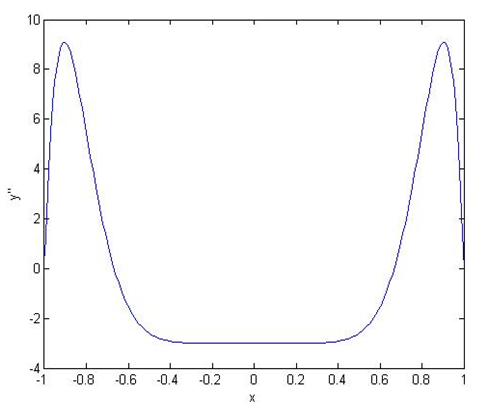
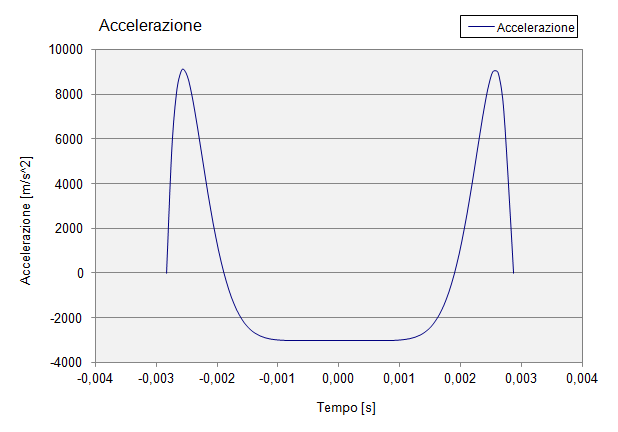
Grafico adimensionale dell’accelerazione del cedente: da tale grafico si ricavano i coefficienti di accelerazione positivo e negativo. I coefficienti Ca+ e Ca– sono definiti come: Ca+ = max (y”) e Ca– = – min (y”). Quindi valutando i punti di massimo e minimo assoluti del grafico si ottengono i seguenti valori: Ca+ = 9,088 Ca– = -3
I valori di tali coefficienti, soprattutto di quello di accelerazione negativa, sono determinanti per la buona progettazione della valvola: da essi dipendono le forze d’inerzia generate durante la fase di apertura e chiusura valvola, quindi indirettamente dipendono le masse del corpo valvola e della molla. Alti valori di Ca– accrescono la probabilità di fenomeni di distacco del piattello dalla camma, il cosiddetto “sfarfallìo”. Per passare dai grafici in forma adimensionale a quelli dell’alzata effettiva Y(t) in funzione del tempo, si utilizzano le formule:
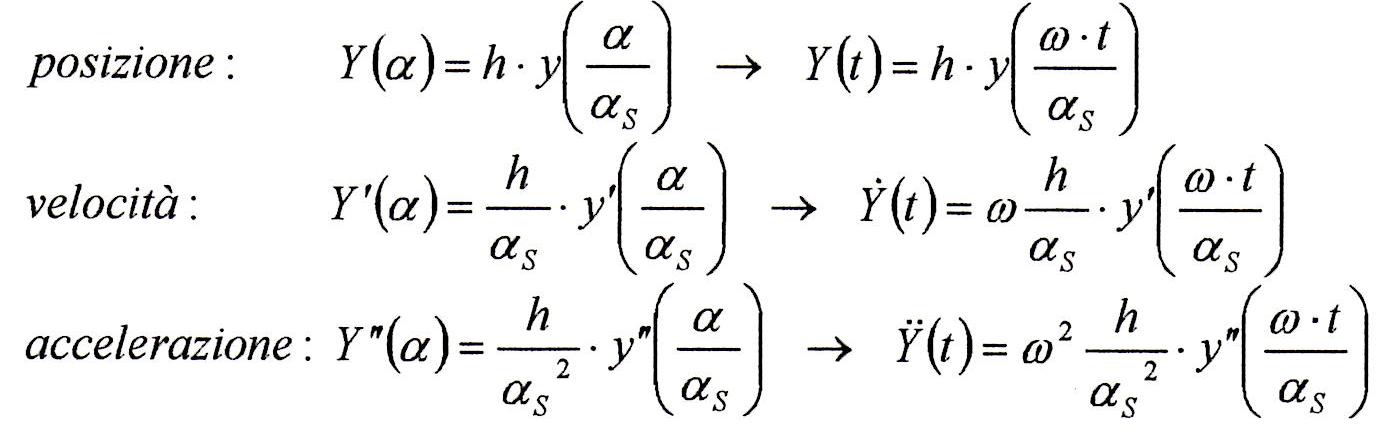
In tutti i grafici effettivi trovati di seguito compariranno valori negativi sull’asse temporale delle ascisse: il significato di tali valori non è puramente fisico, non può esistere tempo negativo, ma legato alla variazione -1<x<+1 dei valori adimensionali dai quali sono stati ricavati i grafici. Rimane la validità dei valori intesa come modulo degli incrementi temporali dt.
Sulla base della legge di moto appena realizzata, ora non ci resta che disegnare l’esatto profilo della camma che permetta l’esecuzione di tale moto e scegliere la molla adeguata per effettuare un corretto accoppiamento con il cedente. In primo luogo è necessario individuare il raggio di base della camma che permetta di ottenere un raggio di curvatura sempre positivo presentando le minori dimensioni possibili, per limitare gli ingombri. In seguito si procede determinando i corretti valori di precarico e rigidezza della molla che permettano di assicurare un contatto costante tra la camma e il piattello senza per questo generare eccessive forze di pressione tra i due corpi, in modo da limitare le dissipazioni e il deterioramento. Per evitare infine che la molla lavori in un campo prossimo alla risonanza, bisogna dimensionare quest’ultima affinché presenti una pulsazione propria a frequenze superiori a quelle di utilizzo.
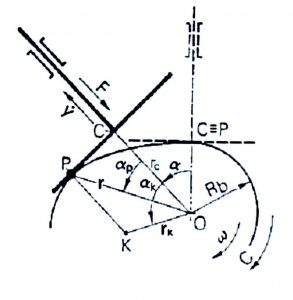
Per una generica posizione angolare α della camma la distanza OC è la posizione voluta della valvola a partire dal raggio base Rb:
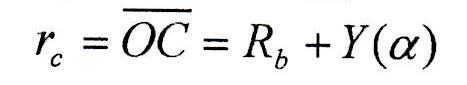
Il punto di contatto P tra camma e piattello non coincide con il centro C di esso. La distanza PC è calcolabile con un bilancio di potenze:
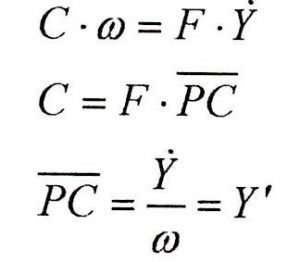
Le coordinate polari del profilo della camma sono perciò date dalle:
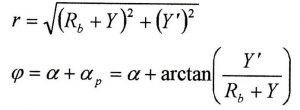
In coordinate cartesiane il profilo della camma è:
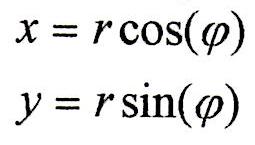
Il raggio di curvatura della camma ρ si ottiene considerando che:
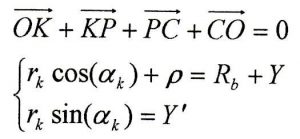
Derivando l’ultima espressione rispetto ad α e tenendo presente che dαk/dα = -1 in quanto il centro di curvatura ha posizione costante per piccole rotazioni allora si ottiene:
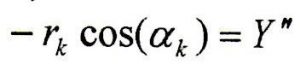
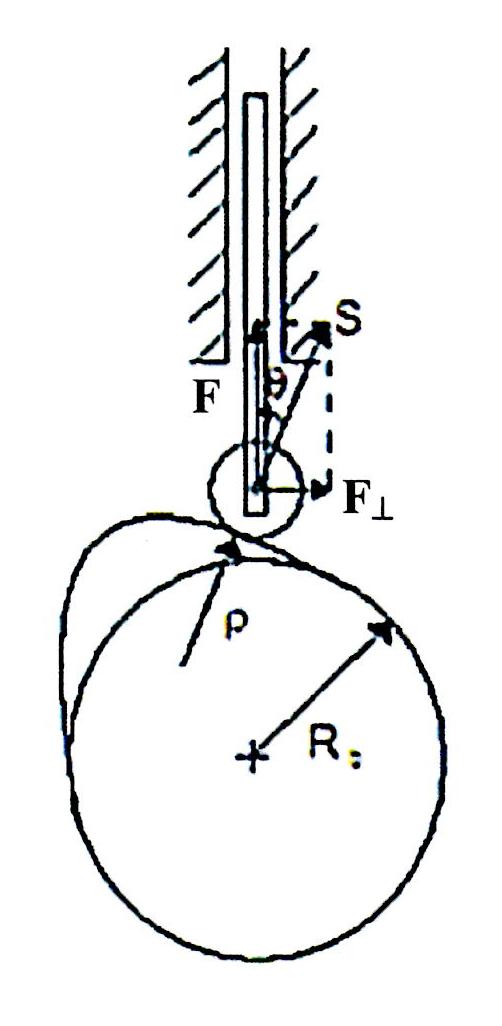
Inoltre, una generica camma deve avere: un angolo di pressione “teta” il più piccolo possibile per ridurre la spinta perpendicolare all’asse del cedente che potrebbe portare al bloccaggio dello stesso; un raggio di curvatura ρ più grande possibile per diminuire le pressioni di contatto tra camma e cedente; un raggio di base Rb piccolo per ridurre le dimensioni della camma. Per camme a punteria con piattello come nel caso in esame, l’angolo di pressione è costante ed è sempre nullo. Il problema è quindi solo sul raggio di curvatura ρ che deve essere sempre maggiore di zero (profilo della camma convesso) perché altrimenti il piattello non può appoggiarsi correttamente sulla camma. Si ricava, infine, il raggio base della camma Rb passando dall’espressione:
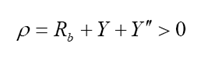
Ed essendo in prima approssimazione Rb >> Y , dalla relazione si può ricavare:
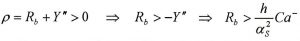
Dalla quale ricaviamo Rb = 28 mm, un valore di primo tentativo per il raggio base. Riportiamo di seguito il grafico del raggio di curvatura in funzione della rotazione dell’albero motore:
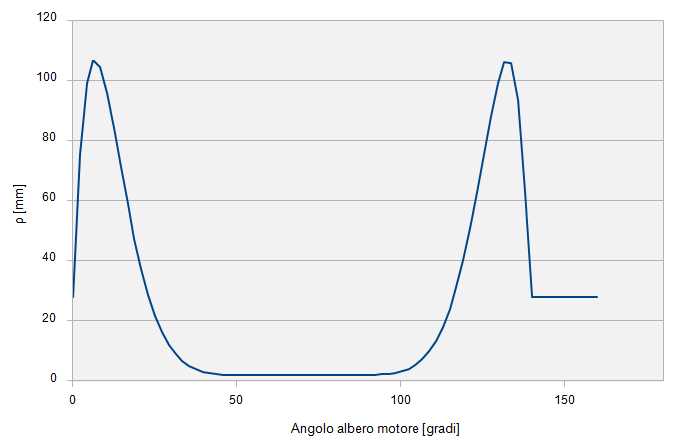
Il profilo della camma definitivo sarà quindi:
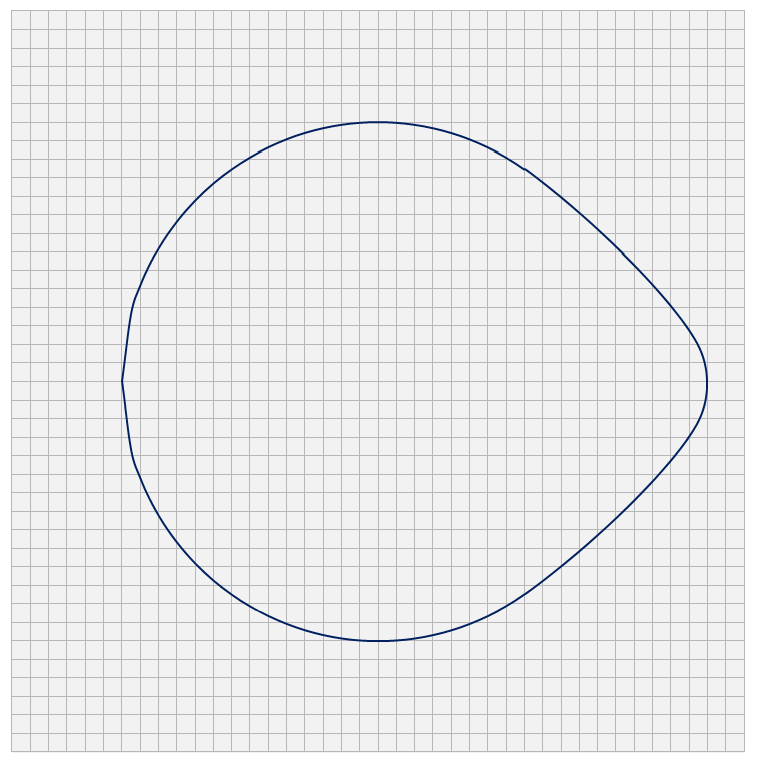
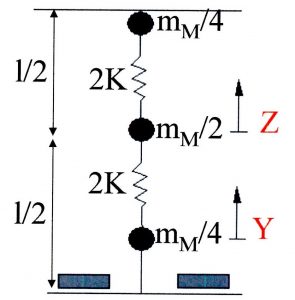
Si passa ora alla determinazione dei corretti valori di precarico e rigidezza della molla che permettano di assicurare un contatto costante tra la camma e il piattello. Per determinare le proprietà di rigidezza di una molla di massa M, utilizziamo un modello equivalente a due gradi di libertà (y,z) costituito da una coppia di molle in serie, ognuna con rigidezza Km = K/2, collegate agli estremi a due masse di valore m = M/4 e al centro con una singola massa di valore m = M/2. Le specifiche riguardanti la massa delle componenti in esame selezionate sono:
| Massa della valvola mv | 90 g |
| Massa della molla mm | 70 g |
Considerando la pulsazione propria della molla ωp troviamo che tale valore deve essere compreso tra le 3 e le 4 volte la pulsazione propria della camma ωcamma. Questo al fine di evitare fenomeni di risonanza tra il sistema molla-valvola e l’albero a camme. Scegliamo quindi un valore di progetto ωp = 3,5 ωcamma, e conoscendo ωcamma = 340 rad/s (velocità di rotazione dell’albero a camme) si ottiene un valore di ωp = 1190 rad/s, con cui può essere facilmente ricavata la rigidezza della molla K dalla relazione:
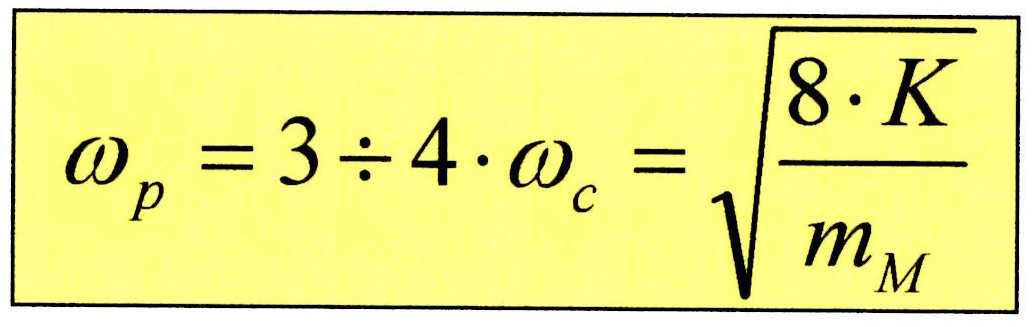
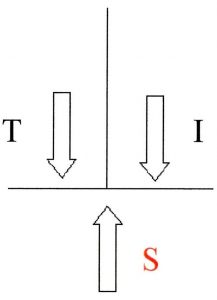
La rigidezza della molla è quindi K = 12390,9 N/mm. Verifichiamo ora le forze agenti sul cedente. Durante la corsa di ritorno, sul cedente agiscono due forze distinte: la forza della molla T e la forza d’inerzia I. Le equazioni che descrivono le due azioni sono:
![]()
Dove m = mv+ (3mm)/8 e T0 è la forza di precarico della molla necessario ad evitare il distacco del cedente dal piattello. Perciò, per non avere il distacco durante la corsa di ritorno, deve valere la condizione I > -T, indicando con I la forza di inerzia massima legata alla valvola. Dal modello a 2 gradi di libertà possiamo ricavare, grazie alla scelta di un K elevato e quindi a condizioni di lavoro lontane dalla risonanza, l’equazione della spinta totale sulla valvola:
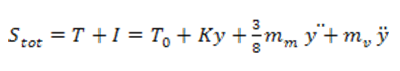
Dalla quale, per avere sempre una forza Stot positiva e verificare quindi la condizione di contatto per ogni angolo di funzionamento, ricaviamo una forza di precarico della molla T = 280 N. Riportiamo ora il grafico della forza d’inerzia Ie della forza T agente sulla molla in funzione dell’angolo di rotazione α:
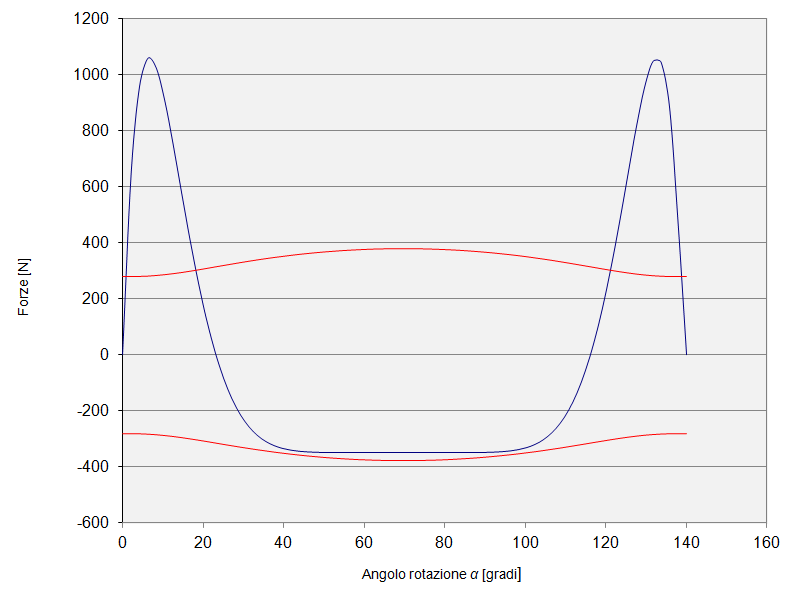
La forza d’inerzia è riportata in blu, in rosso le forze T e –T dovute alla molla. Si noti come nella corsa di ritorno la forza d’inerzia rimanga minore in modulo della forza data dalla molla per tutta la durata della fase, così da assicurare il contatto tra valvola e camma.

Complimenti, articolo fantastico!
Grazie Matteo, sono contento che l’articolo le sia piaciuto.
Complimenti, articolo chiaro e completo!
Grazie, mi fa davvero piacere che le sia piaciuto.
ti sei scordato il jerk, teNNico !!!
Come mi piacerebbe capirci qualcosa…